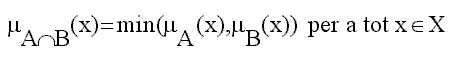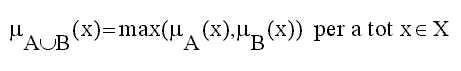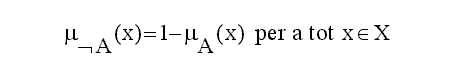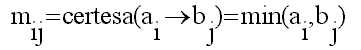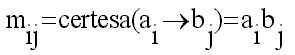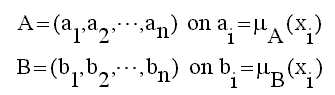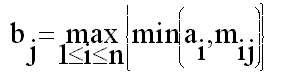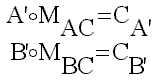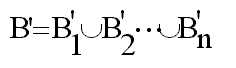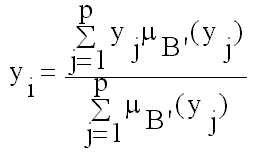Exemple: Temperatura
de l’aigua en una tuberia. Treal=42ºC.
Sistema de mesura:
ºC
Precís i fiable (cert)
: 42 ºC.
Imprecís i fiable
(cert) :
40 - 45ºC.
Precís i poc fiables
(incert) : 47 ºC.
Imprecís i poc fiable
(incert): 22
- 31 ºC.
Percepció humana:
sensació
Imprecisió: “està
bastant calent”.
Imprecisío i incertesa:
“em sembla que esta calent pero no n’estic segur”
Incertesa
i Imprecisió en el Coneixement(II)
-
El tractament d’aquesta inexactitud
(imprecissió i/o incertesa) és un dels objectius de la lògica
difusa.
-
La I.A. tracta la inexactitud
(imprecissió i/o incertesa) en tres passos:
-
En la descripció del
coneixement, informació imprecisa i/o incerta.
Exemple: La temperatura
és alta. (alta és una informació
imprecisa)
-
En la descripció de les
regles que han de raonar respecte aquesta informació.
Exemple: Si la temperatura
és alta estem a l’estiu.
( La regla anterior
pot ser certa o no).
-
En l’avaluació de les
regles (raonament), per deduir noves informacions, i per tant en la descripció
d’aquests nous coneixements.
Exemple: La conclusió
de la regla anterior:
Estem a l’estiu (és
cert o no?).
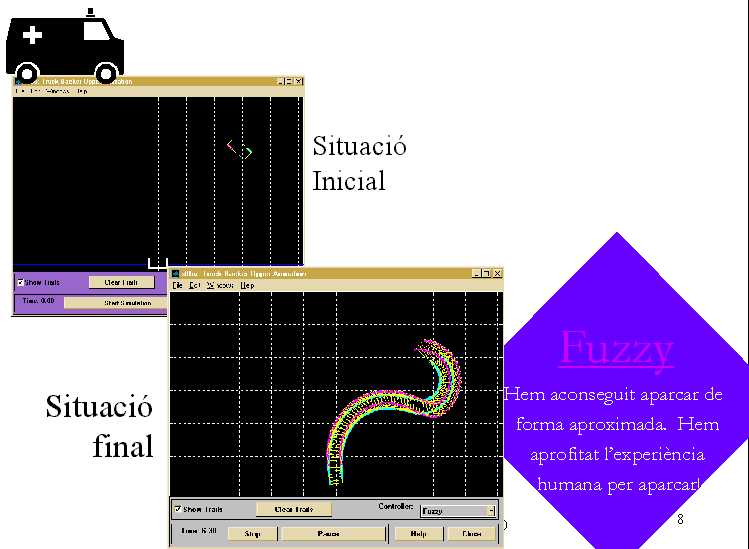
Lògica
Fuzzy: variables
-
És una branca de la lògica
que utilitza graus de pertanyença als conjunts.
-
La lògica binària,
en canvi, només té dos valors possibles per a la pertinença
a un conjunt: cert (pertany) o fals (no pertany).
-
La lògica difusa es centra
principalment en la quantificació i el raonament sobre els termes
imprecisos que apareixen en el llenguatge natural.
-
Aquests termes imprecisos s’anomenen
variables lingüístiques o variables fuzzy.
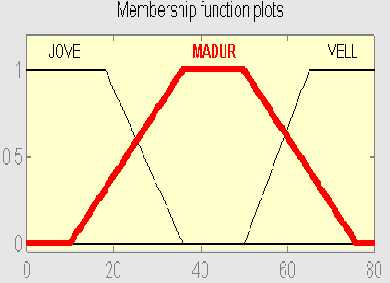
Exemple: temperatura
(fred, tèbi, calent), alçada (baix,normal, alt), velocitat
(lent,normal, ràpid), etc
Lògica
Fuzzy: regles
-
El sistemes basats en la lògica
fuzzy, utilitzen les variables lingüístiques en les regles
fuzzy.
-
Una regla fuzzy infereix informació
sobre una variable lingüística, continguda en la seva conclusió,
a partir de la informació sobre una altra variable, continguda en
la seva premissa.
Exemple:
“SI la velocitat és
lenta LLAVORS fer que l’acceleració sigui alta”
(premissa)
(conclusió)
-
El rang de valors possibles
d’una variable lingüística s’anomena el seu univers de discurs
(X).
Lògica
Fuzzy: Conjunts
-
Sigui X l’univers de discurs
d’una variable fuzzy, essent x els seus elements. Un conjunt fuzzy A sobre
X es caracteritza per una funció de pertinença
que associa a cada element, x, a A amb un grau de pertanyença.
-
La funció de pertinença
es defineix de la següent manera
-
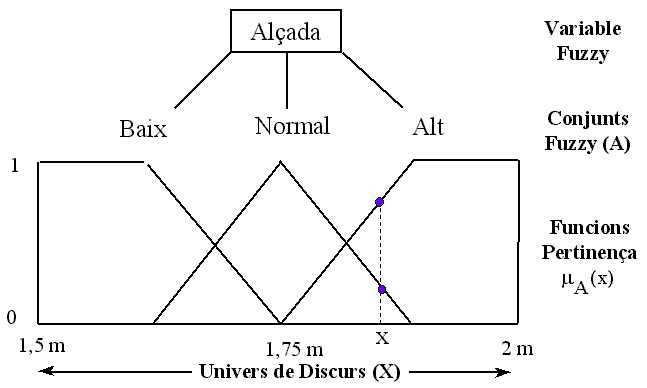
Un conjunt difús es una
extensió d’un conjunt tradicional, generalitzant el concepte de
pertinença mitjançant la funció de pertanyença,
que retorna un valor entre 0 i 1, i que representa el grau de pertanyença
d’un objecte x al conjunt A.
Exemple
de Conjunt Fuzzy
Operacions
entre conjunts fuzzy
-
Intersecció
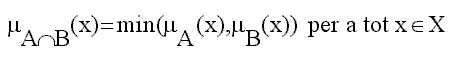
-
Unió
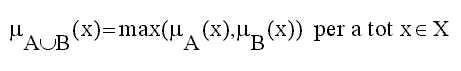
-
Complement
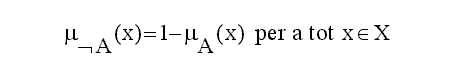
Inferència
Fuzzy: definició (I)
-
En la lògica clàssica
la regla ‘modus ponens’ utilitza pels raonaments (deduccions), les proposicions
següents:
i) y és A
ii) Si y és
A llavors z és B.
per deduir que quan
y és A, z és B.
-
Però que passa si y no
és exactament A, sinó A’? -> lògica fuzzy
-
En la lògica fuzzy, s’aplica
pel raonament el ‘modus ponens generalitzat’, és a dir si coneixem
les premisses:
i) y és
A’
ii) Si y és
A llavors z és B.
podem deduir que
z és B’.
Inferència
Fuzzy: definició (II)
-
La lògica fuzzy tracta
un conjunt fuzzy com una proposició fuzzy, és a dir, una
sentència que a assigna un valor a una variable lingüística,
y:
y és
A,
on A és un conjunt fuzzy sobre l’univers de discurs X.
-
Una regla fuzzy relaciona dues
proposicions fuzzy:
SI x és A LLAVORS
y és B
-
Els motors de inferència
fuzzy emmagatzemen regles com a associacions difuses: així la regla
anterior, s’emmagatzema mitjançant l'associació (A,B) en
la matriu M. Aquesta associació s’anomena Fuzzy Associative Memory
(FAM).
-
Les dues tècniques d’inferència
fuzzy més emprades són: max-min i max-product.
Inferència
Fuzzy: tècniques
La determinació de
la matriu M que conté les associacions difuses definides a través
de les regles del motor d’inferència es pot fer mitjançant:
-
Inferència Max-Min: cadascun
dels elements de la matriu M es determinen
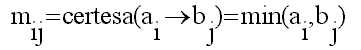
-
Inferència Max-Product:
cadascun dels elements de la matriu M es determinen
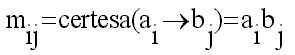
Inferència
Fuzzy: regla d’inferència (I)
-
La inferència del conjunt
difús conclusió a partir del conjunt difús premissa
s’obté a partir de la multiplicació entre vectors i matrius
difusos, a través de l’anomenada regla composicional d’inferència
-
Suposem que aquesta operació
s’aplica a la regla: SI A LLAVORS B, on A es un conjunt fuzzy definit sobre
X i B és un conjunt fuzzy definit sobre Y:
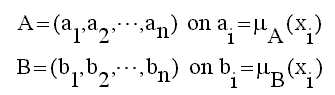
Inferència
Fuzzy: regla d’inferència (II)
-
Sigui M la matriu de regles
fuzzy FAM (determinada prèviament mitjançant la tècnica
max-min o max product), llavors la regla composicional d’inferència
estableix que el conjunt B inferit a partir del conjunt A es determina
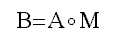
on cadascuna de les components bj es determina
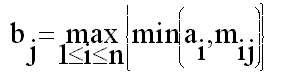
-
Aquesta operació es similar
a la multiplicació clàssica entre vectors i matrius, substituint
el producte pel mínim i la suma pel màxim.
Inferència
fuzzy: regles multipremissa
-
Fins ara hem vist regles del
tipus: IF A THEN B, però a la pràctica s’utilitzen regles
multipremissa: IF A AND B THEN C. Com es determina la matriu M en aquests
casos?
-
La solució consisteix
en definir en primer lloc una matriu M per a cada premissa (per exemple:
MAC i MBC), així:
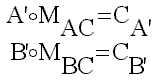
-
Finalment, s’han de composar
els conjunts CA’ i CB’ per obtenir un C’. La composició dependrà
de si les premisses estaven unides amb un AND, o bé, amb un OR.
Inferència
fuzzy: múltiples regles
-
Finalment, considerarem la situació
en la que tenim n regles fuzzy (Ai, Bi). Aquesta situació ens porta
a n matrius M per a codificar les associacions entre Ai i Bi.
-
L’objectiu es obtenir el conjunt
difús B’ a partir del conjunt difús A’: per això aplicarem
A’ al banc de regles produint un conjunt difús B’i per a cadascuna
d’elles.
-
Finalment combinarem cada conjunt
difús B’i fent ús de l’operador unió per obtenir B’:
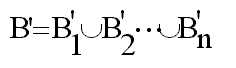
Inferència
fuzzy: defuzzificació
-
Fins ara hem vist com obtenir
un conjunt fuzzy B’ a partir d’un conjunt fuzzy A’. En la majoria d’aplicacions
pràctiques s’ha obtenir un valor a partir del conjunt fuzzy B’.
A aquest procés se l’anomena defuzzificació.
-
La tècnica de defuzzificació
més emprada és el mètode del centre de gravetat fuzzy:
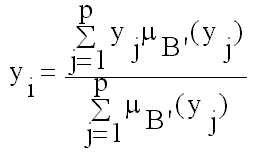
Construcció
d’un sistema fuzzy
Per arribar a construir un
sistema basat en lògica fuzzy s’han de seguir els següents
passos:
1. Definició del
problema
2. Definició de les
variables lingüístiques
3. Definició dels
conjunts difusos
4. Definició de les
regles fuzzy
5. Construcció del
sistema
6. Test del sistema
7. Ajust del sistema
Max-min
versus Max-product (I)
Per una única regla:
max-min
max-product
Max-min
versus Max-product (II)
Per múltiples regles:
max-min
Max-min
versus Max-product (III)
Per múltiples regles:
max-product
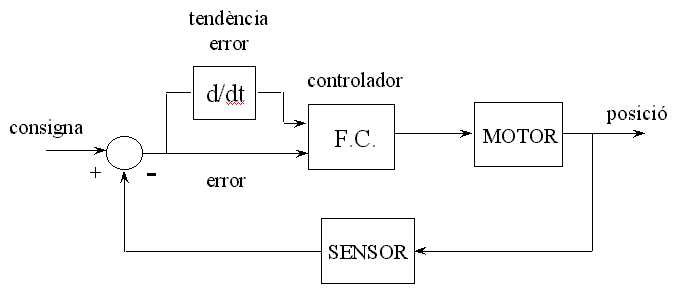
Exemple
d’aplicació: un controlador de posició (I)
1. Definició del problema
Dissenyar un controlador
fuzzy que permeti controlar la posició de l’eix d’un motor. Per
això es disposa de:
+ Sensor que mesura la posició
de l'eix.
+ La variable de control
és la tensió aplicada al motor, amb la que es controla la
velocitat de gir segons:
- tensions positives fan
girar l'eix en un sentit.
- tensions negatives el
fan girar en sentit contrari.
- tensió nul·la
fa aturar el motor.
Exemple
d’aplicació: un controlador de posició (II)
2. Definició de les
variables fuzzy
Les variables que tractarem
de forma fuzzy són:
(a) error (consigna-mesura)
en la posició de l’eix del motor,
(b) velocitat de variació
de l'error de posició
(c) tensió aplicada
al motor (acció).
Exemple
d’aplicació: un controlador de posició (III)
3. Definició dels
conjunts difusos
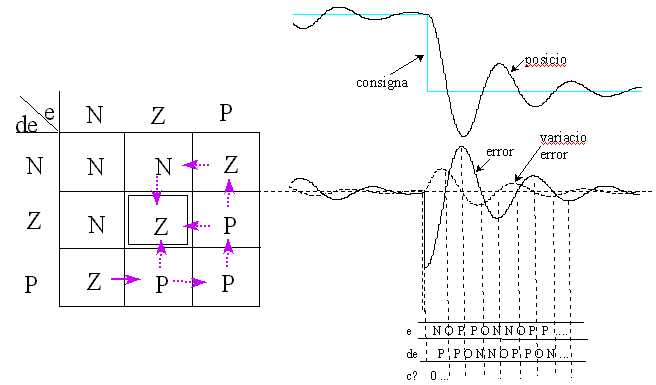
(a) Error: negatiu, zero
o positiu
(b) Variació Error:
negatiu, zero o positiu
(c) Acció control:
negatiu, zero o positiu
Exemple
d’aplicació: un controlador de posició (IV)
4. Definició de les
regles fuzzy
Exemple
d’aplicació: un controlador de posició (V)
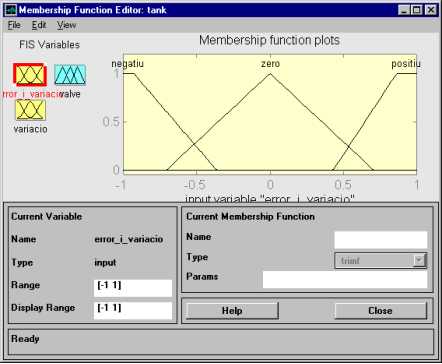
5. Implementació del
controlador
download this document