Objectius de la pràctica:

• Comprensió dels conceptes bàsics del sistemes basats en lògica fuzzy
• Utilització de la Fuzzy Logic ToolBox de MATLAB
• Disseny, prova i ajust d’un sistema de control senzill basat en lògica fuzzy
• Entendre quina és l’aplicabilitat del sistemes basats en lògica fuzzy

1. Descripció del sistema de control a desenvolupar

Com a aplicació dels coneixements adquirits a les sessions teòriques sobre la lògica fuzzy i fent ús de la fuzzy logic ToolBox de MATLAB com eina de treball es proposa dissenyar un sistema de control complex.

• Enunciat del problema de control: definició del problema

 

 

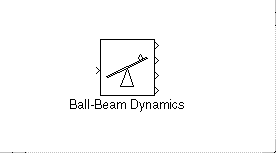
El problema de control consisteix en controlar el parell que aplica un motor sobre una biga suspesa sobre el seu eix de forma que la bola que es troba lliscant sense fregament sobre la superfície es posicioni en la posició desitjada indicada mitjançant la consigna, mantenint la biga en tot moment en posició horitzontal. Es tracta per tant de dissenyar un sistema de regles basat en lògica fuzzy que a partir de la informació proporcionada pels sensors (posició i velocitat de la bola, inclinació i velocitat d’inclinació de la biga) proporcioni el parell que ha d’aplicar el motor sobre la biga per aconseguir els objectius de control fixats: posicionar la bola sobre la biga en la posició escollida mitjançant la consigna mentre es manté la horitzontalitat de la biga. L’esquema del sistema de control a desenvolupar es mostra en la (Fig.1):

Fig.1

• Descripció del procés


La dinàmica del sistema biga-bola es simularà mitjançant el bloc de SIMULINK representat per la (Fig.2). Es pot observar el model d’aquest sistema accedint al diagrama de blocs intern d’aquest bloc. Veure Fig.3.

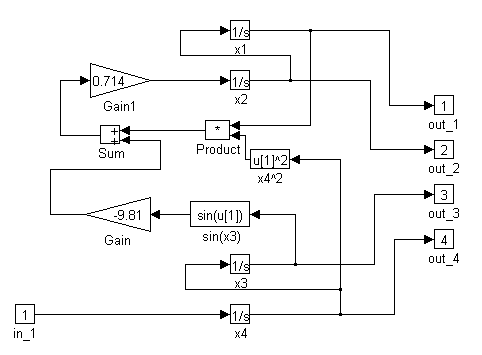
Fig.3

Si tenim en compte que x₁ es la posició de la bola, x₂ és la velocitat amb què es mou la bola sobre la biga, x₃ es la velocitat angular de la biga i x₄ es la inclinació de la biga, a partir del diagrama de blocs anterior podem observar que les quatre equacions matemàtiques que lligen aquestes variables amb l’entrada al sistema, el parell aplicat pel motor a la biga vene donades per:

Equació de la dinàmica de la biga: aquesta equació ens relaciona el parell aplicat a la biga pel motor amb l’accelaració angular que aquesta adquireix

(1)

on: M moment aplicat a la biga, I moment d’inèrcia de la biga i w la velocitat angular de la biga.
Equació de la velocitat angular de la biga: aquesta equació relaciona la velocitat angular amb l’angle d’inclinació de la biga

(2)

Equació de la dinàmica de la bola: sobre la bola s’apliquen dues forces el propi pes de la bola i la força d’inèrcia pel fet de trobar-se sobre la biga que s’està movent a una determinada velocitat angular. L’equació que descriu la dinàmica de la bola és

(3)

on: x és la distància de la bola a l’eix del motor, w és la velocitat angular de la biga, v es la velocitat de la bola i q és l’angle d’inclinació de la bola.

Equació de la velocitat lineal de la bola: aquesta equació relaciona la velocitat lineal de la bola amb l’espai recorregut per la mateixa mesurat respecte a l’eix del motor que mou la biga.

(4)

El model complet que descriu la dinàmica del sistema ademet una representació més compacte utilitzant la representació d’estat. Prenent les següents variables d’estat :

(5)

El model d’estat és el següent:

(6)

 
Tenint en compte la descripció del procés i lenunciat del sistema de control anterior, Es demana :

1. Dissenyar un controlador basat en lògica fuzzy que només controli la horitzontalitat de la biga, independentment de la bola, a partir de les dades de la seva inclinació i velocitat de variació d’aquesta inclinació.

2. Comprovar i ajustar el funcionament del controlador fuzzy.

3. Comparar les prestacions del controlador difús amb les aconseguides amb un controlador tipus PID.

4. Redissenyar el controlador basat en lògica fuzzy perquè a més de mantenir la horitzontalitat de la biga controli la posició de la bola. En aquest cas s’han d’utilitzar quatre variables d’entrada: posició i velocitat de la bola i inclinació i velocitat d’inclinació de la biga.

5. Comparar les prestacions del controlador difús amb les aconseguides amb un controlador tipus PID.

NOTA :

Tot i que el model no contempla restriccions en la llargada de la biga, per l’algorisme de control utilizarem els següents marges en les variables :

Signes  de les variables :

En el model del procés biga-bola de la pràctica es considera un angle nul quan la biga està horitzontal, positu quan aquesta gira en sentit horari i negatiu quan ho fa en senti ani-horari (igualment per les derivades). Pel que fa a la posició de la bola, es considera posició nul·la, el centre de la biga i positiu la part dreta (en posició horitzontal) i negatiu l’esquerra. Tingues en compte en el moment de pensar les rgles que les mesures d’error (de posició i angle) que s’utilitzen en la regulació fuzzy estan calculades com la diferència entre els senyals i la consigna, per conservar el mateix signe per l’error, el senyal i la derivada del senyal).

2. Disseny del sistema de control de la horitzontalitat de la biga

Per començar restringirem el disseny del controlador al cas de disposar només de dues entrades: l’angle de la biga i la posició de la bola, de forma que el nombre de regles que s’hauran d’escriure serà menor. En aquesta situació de control la consigna serà la inclinació de la biga que sempre valdrà zero (horitzontal). Partint de qualsevol situació d’inclinació diferent de zero, el controlador ha d’ésser capaç d’arribar a mantenir la biga horitzontal. Sota aquesta restricció el disseny del sistema de control seguirà les següents etapes:

1. Definició de les variables lingüístiques

Les variables lingüístiques difuses a utilitzar són: l’error de posició de la biga, la seva velocitat d’inclinació i parell aplicat pel motor sobre la biga.

Per a qualificar aquestes variables utilitzarem tres etiquetes.

2. Definició dels conjunts difusos

A continuació associarem una funció de pertinença a cada conjunt difús amb cadascuna de les etiquetes que hagueu definit una funció de pertinença. Per a començar treballarem amb funcions de pertinença triangulars.

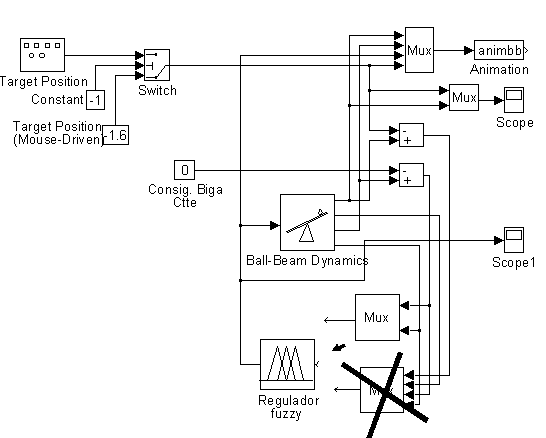
3. Definició de les regles fuzzy

Una vegada definides les variables lingüístiques, els conjunts difusos i les seves funcions de pertinença decidiu quines regles aplicareu per tal de què a partir de la inclinació i de la seva velocitat de variació d’aquesta inclinació el vostre controlador fuzzy sigui capaç de generar una acció de control que mantingui la biga sempre en horitzontal.

4. Construcció del sistema

Per a construir el sistema fuzzy utilitzeu les eines que ens proporciona la fuzzy logic ToolBox de MATLAB: bàsicament les eines, FIS editor, membership function editor i rule editor.

5. Prova del sistema

Pera provar el sistema es proposa utilitzar el SIMULINK junt a la simulació del dipòsit d’aigua. Utilitzeu el visualitzador de regles ("rule viewer") i de superfícies ("surface viewer") per a interpretar el funcionament del controlador basat en lògica fuzzy.

6. Ajust del sistema

Jugant amb els pesos associats a les regles, a les formes de les funcions de pertinença associades al conjunts difusos, amb el nombre de conjunts, etc. intenteu millorar les prestacions del controlador aconseguides a l’apartat anterior.

Comparació amb un Controlador tipus PID

Finalment es proposa comparar les prestacions del controlador basat en lògica fuzzy que heu construir amb les que obtingudes amb un controlador clàssic tipus PID. Es proposa, doncs, d’ajustar un controlador tipus PID per tal de controlar la horitzontalitat de la biga.

 
3. Disseny del sistema de control de la posició de la bola

Una vegada dissenyat el controlador d’horitzontalitat, anem a modificar-lo per tal de què pugui controlar també la posició de la bola. En aquest cas de disposarem de quatre entrades: posició i velocitat de la bola, inclinació i velocitat d’inclinació de la biga.

1. Definició de les variables lingüístiques

Les variables lingüístiques difuses a utilitzar són: la posició de la biga, la seva velocitat d’inclinació, l’error de posició de la bola i la seva velocitat com a variables d’entrada i parell aplicat pel motor sobre la biga com a variable de sortida.

Per a qualificar aquestes variables utilitzarem tres etiquetes.

2. Definició dels conjunts difusos

A continuació associarem a cada conjunt difús associat amb cadascuna de les etiquetes que hagueu definit una funció de pertinença. Per a començar treballarem amb funcions de pertinença triangulars.

3. Definició de les regles fuzzy

Una vegada definides les variables lingüístiques, els conjunts difusos i les seves funcions de pertinença decidiu quines regles aplicareu per tal de què: a partir de la inclinació i de la seva velocitat de variació d’aquesta inclinació el vostre controlador fuzzy sigui capaç de generar una acció de control que mantingui la biga sempre en horitzontal i aconsegueixi situar la bola a la posició desitjada

4. Construcció del sistema

Per a construir el sistema fuzzy utilitzeu les eines que ens proporciona la fuzzy logic ToolBox de MATLAB: bàsicament les eines, FIS editor, membership function editor i rule editor.

5. Prova del sistema

Pera provar el sistema es proposa utilitzar el SIMULINK junt a la simulació del sistema biga-bola. Utilitzeu el visualitzador de regles ("rule viewer") i de superfícies ("surface viewer") per a interpretar el funcionament del controlador basat en lògica fuzzy.

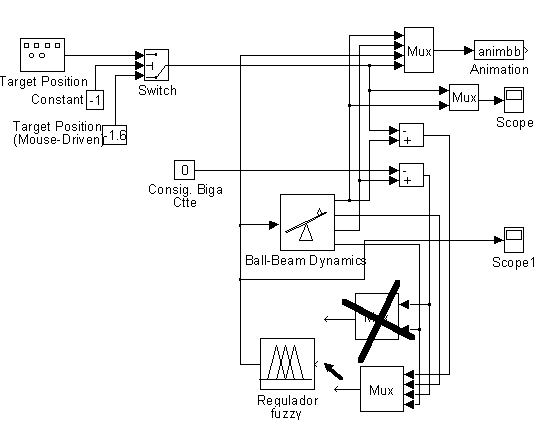
6. Ajust del sistema

Jugant amb els pesos associats a les regles, a les formes de les funcions de pertinença associades al conjunts difusos, amb el nombre de conjunts, etc. intenteu millorar les prestacions del controlador aconseguides a l’apartat anterior.

(Optatiu) Comparació amb un Controlador tipus PID

Finalment es proposa comparar les prestacions del controlador basat en lògica fuzzy que heu construir amb les que obtingudes amb un controlador clàssic tipus PID. Es proposa, doncs, d’ajustar un controlador tipus PID fent servir el mètode d’ajust que desitgeu (qualsevol dels que hagueu après anteriorment) i comparar els resultats obtinguts amb el controlador basat en lògica fuzzy. En aquest cas donat que el que es vol es controlar és tan l’horitzontalitat com la posició de la bola en calgui més d’un controlador PID. Penseu quants en calen i proveu-ho.