Xarxes Neuronals

Introducció

• El camp de les xarxes neuronals constitueix una tècnica de tractament de la informació basada en estudis sobre el funcionament del cervell i del sistema nerviós humà.
• Després de caure en decadència durant els anys 70, el camp de les xarxes neuronals va ressorgir amb molta força cap els anys 80.
• Aquest renovat interès per les xarxes neuronals s'explica per la necessitat de disposar de tecnologies de tractament de la informació que funcionessin de forma similar al cervell humà, a l'avanç en la tecnologia dels ordinadors i al progrés en el coneixement del funcionament del cervell.

 

 

Analogia Biològica
 

• El cervell humà està composat d'unes cèl·lules especials anomenades neurones. Les neurones formen grups anomenats xarxes. Cada xarxa conté mils de neurones i estan altament interconnectades, per tant, el cervell humà es pot veure com una col·lecció de xarxes neuronals.
• Una xarxa neuronal artificial és un model que simula una xarxa neuronal biològica

 

 

Fonaments de les X.N.: Components
 

• Una X.N. està composada d'unitats de processament (equivalents a les neurones) organitzades de diferents formes tot formant l'estructura de la xarxa.
• Les unitats de processament reben una o varies entrades, les processen i generen una sola sortida. Les entrades poden ser dades directes o bé sortides d'altres unitats. La sortida pot ser el resultat final, o bé, l'entrada d'una altra unitat de processament.

 

 

Fonaments de les X.N.: Components d'una neurona.



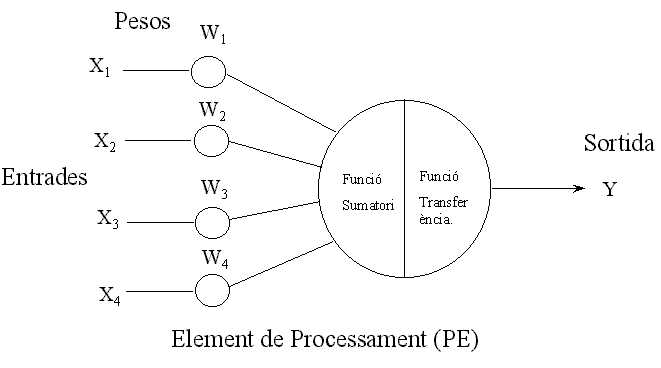
Estructura d'una XN



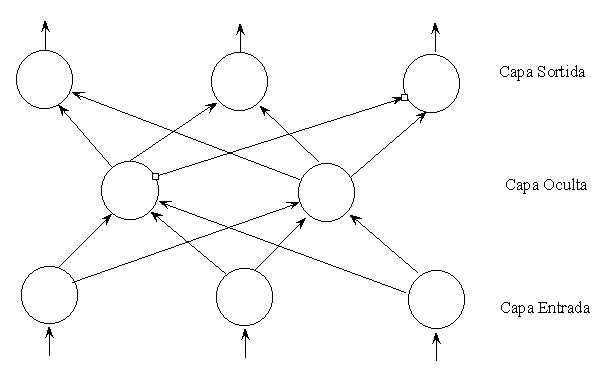
Processament de la Informació: Entrades
 

• Cada entrada correspon a un atribut individual. El valor numèric de l'atribut és l'entrada a la xarxa.
• Les xarxes neuronals només poden processar números. Si per resoldre un problema la xarxa ha de treballar amb valors qualitatius o imatges, aquests s'han de preprocessar fins a convertir-los en un format numèric equivalent.
• Exemples d'entrades a xarxes neuronals poden ésser: valor dels pixels de caràcters o d'altra tipus de gràfics, imatges o veu digitalitzades, senyals digitalitzats provenint de sensors d'un sistema de monitorització, etc.

 

 

Processament de la Informació: Sortides
 

• La sortida de la xarxa és la solució del problema. Per exemple, en el cas d'utilitzar una XN per a reconeixement de caràcters la sortida seria el valor del caràcter reconegut.
• Un element clau en una XN són els pesos. Els pesos expressen la importància relativa de cada entrada a la unitat de processament. És mitjançant l'ajust dels pesos que la xarxa aprèn.
• La funció sumatori calcula la suma ponderada de totes les entrades que entren a un element de processament, multiplicant cada valor d'entrada Xi pel seu pes Wi

 

 

Processament de la Informació: Funció sumatori
 

• La funció sumatori calcula la suma ponderada de totes les entrades que entren a un element de processament, multiplicant cada valor d'entrada Xi pel seu pes Wi. La formula per n entrades a un element de processament és

 

 


 

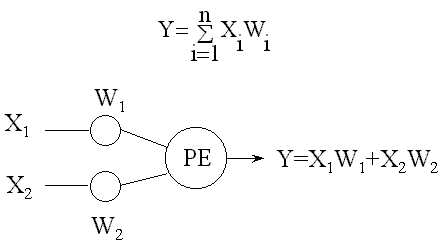
Processament de la Informació: Funció Transferència
 

• La funció sumatori calcula el nivell d'activació de la neurona. A partir d'aquest nivell, la neurona pot produir, o no, una sortida. La relació entre el nivell d'activació i la sortida s'expressa mitjançant una funció de transferència. Una de les funcions de transferència més emprades és la funció sigmoidal

 

 



    on YT és el valor transformat de Y.

• L'objectiu de la transformació és normalitzar el valor de sortida. Aquesta transformació es pot aplicar a la sortida de cada neurona, o bé, de la xarxa

 

 

Aprenentatge de la XN: Procés
 

• Una XN aprèn a partir de la seva experiència. El procés d'aprenentatge implica les següents tasques:
• Càlcul de les sortides
• Comparació de les sortides amb els valors desitjats
• Ajust dels pesos i repetició del procés
• El procés d'aprenentatge comença fixant  els pesos mitjançant alguna regla, o bé, aleatòriament.
• La diferència entre el valor actual i el desitjat s'anomena delta. L'objectiu és minimitzar la delta.
• La reducció de la delta s'aconsegueix canviant el valors dels pesos en la direcció adequada.
• Existeixen multitud d'algorismes d'aprenentatge

 

 

Aprenentatge Supervisat
 

• Utilitza un conjunt d'entrades per les quals les sortides (desitjades) són conegudes.
• La diferència entre la sortida actual i la desitjada s'utilitza per a calcular les correccions dels pesos de la XN.
• Exemples de d'aquest tipus d'aprenentatge són la Xarxa de Hopfield i el Backprogragation

 

 

Aprenentatge No Supervisat
 

• Només es mostra una entrada a la XN. La xarxa s'autoorganitza, és a dir, s'organitza internament de manera que els elements de processament interns responen estratègicament a diferents entrades.
• No es proporciona cap coneixement quines classificacions són correctes, així com les classificacions que obté la XN poden o no tenir significat per a la persona que l'està entrenant.
• Encara que el nombre de categories en que la xarxa classifica les sortides es pot controlar variant determinats paràmetres del model. De tota manera, la persona que ha entrenat la XN ha d'examinar les categories finals el significat a cadascuna d'elles i determinant la utilitat dels resultats obtinguts.
• Exemples d'aquest aprenentatge són ART (Adaptive Ressonance Theory) i els mapes autoorganitzatius de Kohonen

 

 

Classificació dels Algorismes d'Aprenentatge



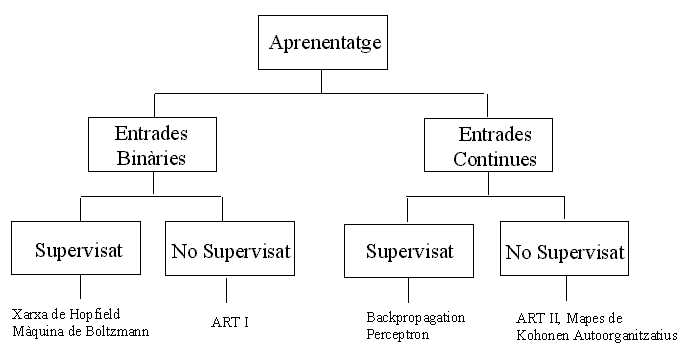
Com aprèn una XN? (I)
 

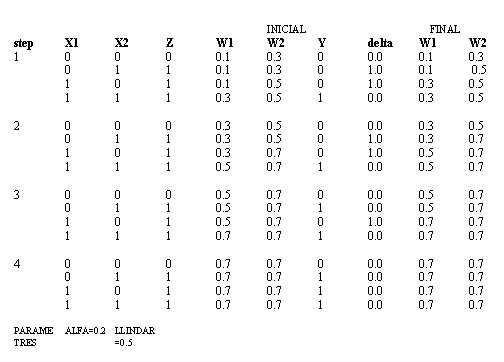
• Considerem una XN amb una sola neurona que volem que aprengui la taula de l'operació lògica OR
• La XN té dues entrades X1 i X2. Si qualsevol de les dues entrades té un valor positiu, aleshores volem que la sortida Y sigui també positiva. En cas contrari, volem que sigui 0.
• La neurona ha d'ésser entrenada per tal que reconegui els patrons d'entrada i els classifiqui adequadament assignant-te'ls-hi la sortida corresponent.
• El procediment d'aprenentatge consisteix en presentar a la neurona una seqüència de quatre patrons d'entrada de manera que els pesos s'ajustin a cada iteració.
• Aquest procés es repeteix fins que els pesos convergeixen a un conjunt uniforme de valors que permeten a la neurona classificar correctament les quatre entrades

 

 

Com aprèn una XN? (II)
 

• En el nostre exemple, després de calcular les sortides, s'utilitza una mesura de l'error (delta) entre la sortida i el valors desitjats per actualitzar els pesos.
• En qualsevol instant del procés d'aprenentatge per una neurona j:

delta = Zj-Yj
       on Z i Y són les sortides desitjades i actual respectivament. Aleshores, els pesos actualitzats són:
Wi(final)=Wi(inicial) + alpha * delta * Xi
     on alpha és una paràmetre que controla la velocitat d'aprenentatge.
• A la regla d'actualització dels pesos se l'anomena llei d'aprenentatge.

 

 

Com aprèn una XN? (III)



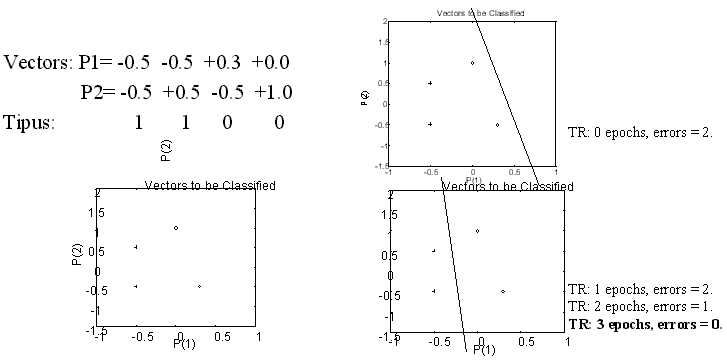
Exemple 1: Classificació de vectors



Backpropagation (I)
 

• És l'algorisme d'aprenentatge més utilitzat en el camp de les XN, i a la vegada es relativament fàcil d'implementar.
• Una XN de backpropagation utilitza una o més capes ocultes i a més és del tipus feedforward, ja que no hi ha interconnexió entre la sortida de la XN i l'entrada de les neurones de les capes de sortida o de capes anteriors
• A partir de la capa de sortida, els errors entre la sortida actual i la desitjada s'utilitzen per a corregir els pesos de les connexions de la capa anterior.
• Per una neurona de sortida qualsevol j, l'error val:

delta = (Zj-Yj) * (df/dx)
    on Z i Y són les sortides actual i desitjades de la XN

Backpropagation (II)
 

• És útil escollir la funció sigmoidal f = [1+exp(-x)]-1 per a representar la sortida d’una neurona, on x es proporcional a la suma ponderada de les entrades a la neurona. De manera que, df/dx = f·(1-f) i l'error és una funció simple de les sortides actual i desitjada.
• El factor f·(1-f) es la funció logística, que serveix per a mantenir la correcció de l'error acotada.
• Els pesos de cadascuna de les entrades de la j-èsima neurona es canvien llavors de forma proporcional a aquest error calculat d'aquesta manera.
• Anàlogament es pot calcular l'expressió que transfereix l'error de la sortida a l'actualització dels pesos de les capes interiors

 

 
 
 
 
 

download this document