
Fig. 1 Perceptró: model d’una neurona
|
"XARXES NEURONALS: APLICACIÓ AL RECONEIXEMENT DE PATRONS" |
Objectius de la pràctica:
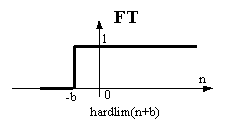
1. El Perceptró: una xarxa neuronal simpleLa neurona d’un perceptró, que té com a funció de transferència (FT) un limitador, es mostra en la Fig. 1. El codi MATLAB que permet calcular la sortida d’aquesta neurona es presenta també en la mateixa figura.

Cada entrada es ponderada amb el correspoent pes W, i la suma de les entrades ponderades és enviada a la funció de transferència de tipus limitador. Aquesta funció de transferència, que MATLAB l’anomena hardlim, retorna un "0", o bé, un "1" depenent de quin és el rang de l’entrada. La representació gràfica d’aquest comportament es pot veure en la Fig. 2. Es pot veure com el llindar d’activació es pot variar afegint una constant, b. Aquest paràmetre s’anomena ‘offset’ o ‘bias’ (b).
Una xarxa neuronal formada per neurones de tipus perceptró està formada per una sola capa amb S neurones tipus perceptró connectades a R entrades a través d’un conjunt de pesos W(i,j) tal com es mostra en la Fig. 3. Els indexos "i" i "j" indiquen que el pes W(i,j) es el pes de la connexió de la j-èsima entrada de la i-èsima neurona (per tant de la i-èsima component de la sortida de la xarxa).
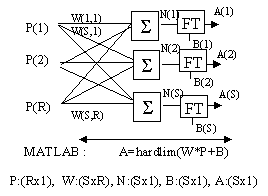
Fig. 3 Xarxa neuronal formada per perceptrons (FT es hardlim, Fig.2)
1.1 InicialitzacióLa funció rands s’utilitza per inicialitzar els pesos a valors aleatoris. Així per exemple, una xarxa neuronal formada per 8 neurones i 4 entrades s’inicialitzaria mitjançant
R=4; S=8; [W,B]=rands(S,R); % R i S son les dimensions del vector d’entrada i sortida resp.
Una xarxa neuronal formada per perceptrons és entrenada perquè respongui davant d’un vector d’entrada amb el corresponent vector objectiu de sortida, els elements del qual son un "0", o bé, un "1". La regla d’aprenentatge és aplicada a cada neurona per tal de determinar el nou conjunt de valors dels pesos després de la darrera presentació de les entrades a la xarxa. Els canvis en els elements de la matriu de pesos es calcula mitjançant la funció de MATLAB learnp, que retorna el canvis sobre la matriu de pesos a partir del vector d’entrades P, el vector de sortides A (calculat a partir del vector de pesos abans d’actualitzar els pesos) i el vector de sortides objectiu T
A continuació es presenta el codi MATLAB que presenta a un perceptró un vector entrades P i actualitza els pesos mitjançant la regla d’aprenentatge i el vector de sortides objectiu T
[dW,dB]=learnp(P,A,T);
W=W+dW;
B=B+dB;
"per tot i, ...
Aquestes operacions es poden resumir en les següents equacions:
![]()
Els vectors patró són presentats a la xarxa neuronal un darrera de l’altre. Si la sortida de la xarxa és correcta no s’aplica cap canvi. En cas contrari, els pesos i els offsets s’actualitzen utilitzant la regla d’aprenentatge del perceptró. Quan s’ha presentat el conjunt de tots els patrons diem que s’ha finalitzat una època (epoch). Si després de presentar el conjunt de tots els patrons cap d’ells presenta error, l’entrenament finalitza. En aquest moment, si es presenta qualsevol entrada patró a la xarxa aquesta respondrà amb la sortida objectiu desitjada. Si un vector Pi que no està contingut en el conjunt d’entrenament es presenta a l’entrada de la xarxa aquesta intentarà generalitzar responent amb una sortida similar al vectors objectiu corresponents als vectors patró d’entrada que més s’assemblin al vector d’entrada Pi.
El codi MATLAB per entrenar un perceptró és
el següent:
MATLAB disposa d’una funció que realitza tot
el procés d’entrenament presentat amb el codi anterior d’una sola
vegada. Aquesta funció és la funció trainp.
1.4 Exemple d’aplicació: implementació de la funció lògica OR
Fent ús de tota la informació presentada
fins el moment es demana entrenar una xarxa neuronal formada per una sola
neurona de tipus perceptró per tal de què aprengui el funcionament
de la funció lògica OR.
Sortides desitjades
T(1, :) : 0 1 1 1 matriu T = [0 1 1 1] ;
2. Backpropagation: un mecanisme d’aprenentatge eficient
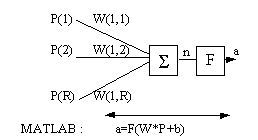
Una neurona d’una xarxa de backpropagation amb R entrades es pot representar simbòlicament mitjançant la Fig. 4. Cada entrada és ponderada amb un pes W. La suma de les entrades ponderades, junt amb un offset, constitueixen l’entrada de la funció de transferència F. Les neurones d’una xarxa de backpropagation poden utilitzar qualsevol funció F diferenciable per a generar la sortida de la xarxa
Les xarxes de backpropagation utilitzen sovint la funció de transferència log-sigmoidal que en MATLAB s’implementa mitjançant la funció logsig. La representació gràfica d’aquesta funció de transferència es presenta en la Fig. 5. La funció logsig genera sortides entre 0 i 1 al variar l’entrada de la neurona des de valors positius a valors negatius. Aquesta funció de transferència es pot utilitzar amb offset, o bé, sense. Els offsets ofereixen a la xarxa un grau de llibertat més alhora d’aprendre el comportament d’una determina funció. La seva utilització augmenta les possibilitats de què la xarxa trobi una solució acceptable, mentre que a la vegada redueixen el nombre d’èpoques d’aprenentatge necessàries.
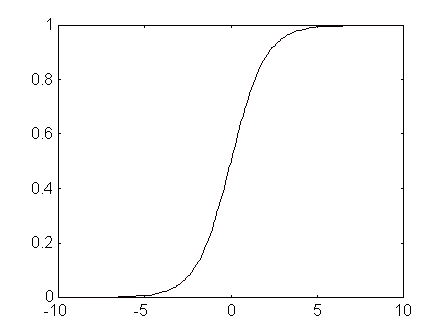
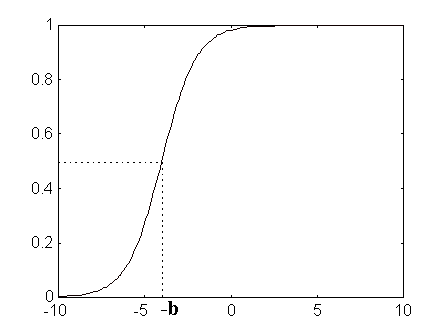
Fig. 5 Backpropagation: funció de transferència logsig (n) i logsig(n+b) .
De forma alternativa, les xarxes de backpropagation poden utilitzar la funció de transferència (F) tan-sigmoidal implemanta en MATLAB amb la funció tansig. Aquesta funció es presenta en la Fig. 6.
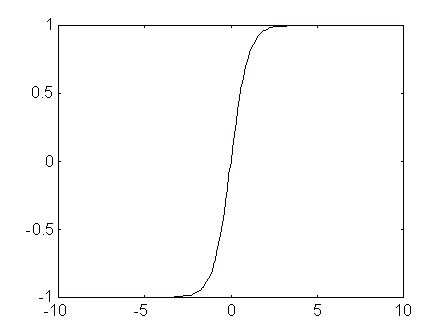
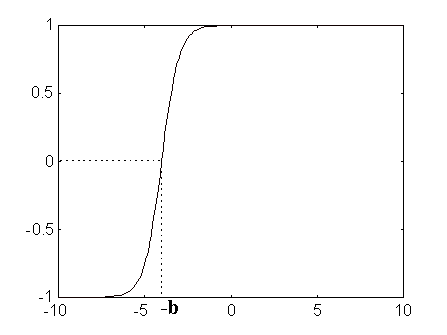
Fig. 6 Backpropagation: funció de transferència tansig(n)i tansig(n+b).
De vegades, també es pot utilitzar la funció de transferència lineal que el MATLAB implementa amb la funció purelin. Aquesta funció es presenta en la Fig. 7.
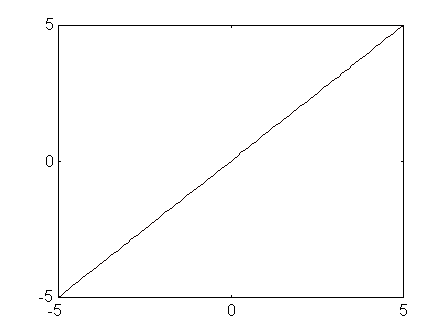
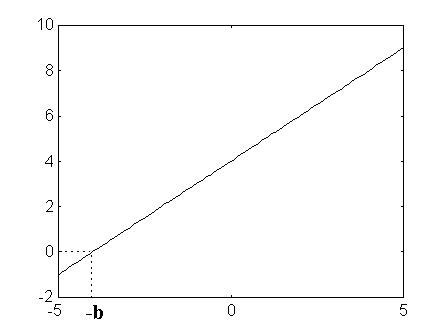
Fig. 7 Backpropagation: funció de transferència purelin(n) i purelin(n+b)
En la Fig. 8 es presenta una xarxa neuronal amb S neurones log-sigmoidals amb R entrades. Les xarxes de backpropagation sovint tenen una o més capes ocultes de neurones sigmoidals seguides per una capa de sortida de neurones lineals. Múltiples capes de neurones amb funcions de transferència no lineals permeten a la xarxa l’aprenentatge de relaciones lineals i no lineals entre l’entrada i la sortida.
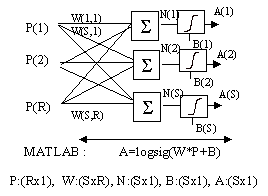
Fig. 8 Backpropagation: estructura d’una xarxa neuronal d’una capa
En el cas d’utilitzar xarxes amb múltiples capes, afegirem el numero de la capa als noms de les matrius i vectors associats amb la capa. Així, la matriu de pesos i el vector de sortides de la capa 2 d’una xarxa s’anomenaran W2 i A2 respectivament. En la Fig. 9 es presenta una xarxa de backpropagation amb dues capes una tan-sigmoidal i una altra de lineal que fan servir aquesta notació.
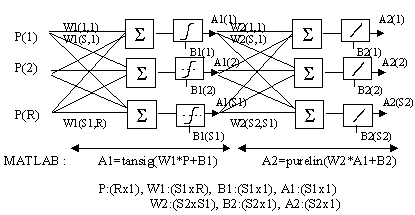
Fig. 9 Backpropagation: estructura d’una xarxa neuronal de dues capes
2.1 InicialitzacióLa inicialització de la matriu de pesos d’una xarxa de backpropagation es fa amb valors aleatoris entre -1 i 1. Aquesta inicialització aleatòria es pot fer mitjançant la funció de MATLAB rands. Així, per exemple, per una xarxa neuronal de backpropagation de dues capes, amb 5 entrades, 4 neurones a la capa oculta i 3 neurones a la capa de sortida, que sera entrenada amb els patrons P (entrades) per obtenir les sortides T, el codi d’inicialització és el següent. Les matrius d’entrada i de sortides desitjades (P i T) estan formades per:
P : Matriu amb Q vectors columna de 5 components. (R=5)T : Matriu amb Q vectors columna de 3 components (S2=3)
on Q son el número de vectors que s’utilizaran en l’entrenament i per tant el mateix número de vectors de sortida (objectiu) per comparar amb les sortides de la xarxa.
Així el codi Matlab serà :
Cal observar que el nombre d’entrades de la xarxa i el nombre de neurones en la capa de sortida ve fixat pels vectors entrada/objectiu que la xarxa ha d’aprendre. El número de neurones en les capes ocultes es decisió del dissenyador de la xarxa. Quantes més neurones, més possibilitat de què la xarxa assoleixi una solució. En canvi, quantes més neurones més temps d’aprenentatge serà necessari i més grans seran les matrius de pesos. [R,Q]=size(P);
S1=4; % 4 neurones capa oculta
[S2,Q]=size(T); %
[W1,B1]=rands(S1,R); % Pesos i bias capa oculta
[W2,B2]=rands(S2,S1); % pesos i bias capa de sortida2.2 Regla d’aprenentatge
La regla d’aprenentatge donada per l’algorisme backpropagation permet l’entrenament de xarxes no lineals multicapa per a aplicacions de classificació i associació de patrons. La restricció d’aquest algorisme és que les funcions de transferència (o activació) han de ser funcions derivables, ja que l’ajust dels pesos es fa seguint una algorisme de minimització de l’error quadràtic mig (LMS, Least mean squared) mitjançant la disminució del gradient (‘gradient descent’) a cada iteració efectuada per l’ajust dels pesos. Per això és necessari calcular les derivades de l’error (vector delta). I l’error es defineix com la diferència entre les sortides teòriques i les reals).
Les derivades de l’error calculades a la sortida de la última capa (ja que és la única que podem comparar amb els patrons desitjats), es propaguen cap a les capes internes (ocultes). A Matlab el càlcul dels delta vectors (D) es fa amb les funcions deltalin(A,E), deltalog(A,E) i deltatan(A,E) en el cas de la capa oculta i deltalin(A,D,W), deltalog(A,D,W), deltatan(A,D,W) pel cas de capes ocultes. Els paràmetres corresponen a : A : vector de sortides, E : vector error, D i W : són els delta vectors i els pesos de la capa anterior. S’utilitza una funció o altra d’acord amb la funció de transferència desitjada en cada capa.A mesura que es va propagant l’error cap a les capes ocultes, l’actualització dels pesos (i bias) es fa segons aquests valors seguint amb els increments calculats d’aquesta forma:
DW(i,j)= lr D(i)P(i) lr : velocitat d’aprenentatge.
DB(i)= lr D(i) D(i) : vector delta propagat.
P(i) : Entrades de la cpa en qüestió.
La funció de Matlab [dW,dB]=learnbp(P,D,lr) es pot utilitzar amb aquest propòsit. Només cal tenir en compta que P i D s’han de presentar com matrius, amb els vectors columnes corresponent a tots els patrons que es volen entrenar.
E1cas contrari es calcula el vector delta a la sortida de la xarxa i es propaga enrera (backpropagation) cap ales capes ocultes. A partir dels vecors delta de cada capa s’actualitzen els pesos d’acord amb la regla d’aprenentatge anterior. I es repeteix el procés fins que l’error sigui inferir a un llindar predeterminat.
Aquest procediment es pot fer de froma c`moda a Matlab utilitzant la funció trainbp que permet l’entrenament de xarxes de varies capes. En aquest cas cal els passos a seguir son :
Per cada capa caldrà a més a més
:
- Inicialitzar (aleatoriament) les matrius W i B de pesos
i bias.
- Especificar el tipus de xarxa (funció de transferència)
en un string. ‘Fx’ per exemple.
Amb tot això podem fer crides ala funció anterior com la següent, pel cas d’una xarxa de dues capes :
[W1,B1,W2,B2,epochs, TR]=trainbp(W1,B1,’F1’,W2,B2,’F2’,P,T,TP)
;
2.4 Exemple d’aplicació: aproximació d’una funció matemàtica qualsevol
Finalment, una vegada presentat com el MATLAB tracta les xarxes neuronals de backpropagation es proposa d’utilitzar una d’aquestes xarxes per aproximar el comportament d’una funció no lineal donada per l’expressió en el marge -1<t<1:
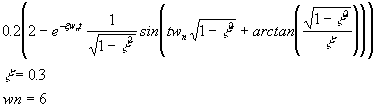
Per aixo es prendran 21 mostres de la variable t, distribuïdes entre -1 i 1 equiespaiades 0’1 unitats entre elles. Aquests 21 mostres s’utilitzaran com senyals d’entrada de la xarxa. Es pretén per tant que la xarxa sigui capaç d ‘aproximar aquesta funció. Per tant s’entrenarà la xarxa de forma que per les entrades proposades donin les sortides corresponents a la funció anterior.
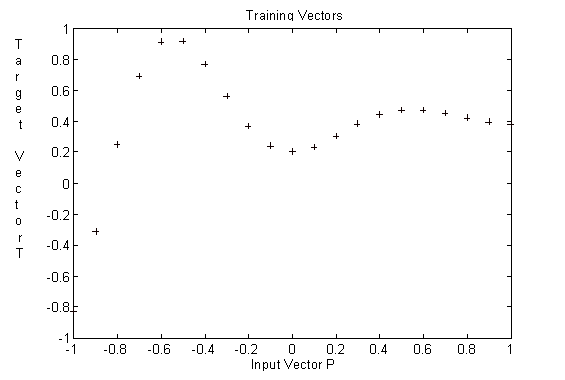
Fig. 10 Relacio entre patrons de l’entrada i sortides desitjades.
Codi Matlab per representar la funció :t= -1:.1:1;
psi=0.3;
wn=6;
wd=wn*sqrt(1-psi^2);
P = t ; % Patrons de l’entrada
T=0.2*(2-exp(-psi*wn*P)/sqrt(1-psi^2).*sin(wd*P+atan(sqrt(1-psi^2)/psi)));% sortides desitjades% corresponents a les 21
% entrades anteriors.
Estructura de la xarxa :
La xarxa neuronal proposada es dissenyarà amb una entrada, una sortida i dues capes. La primera capa (capa oculta) tindrà 5 neurones d’una sola entrada amb funció de transferència tansigmoidal i la segona capa una única neurona de 5 entrades i funció de transferència lineal (veure figura).
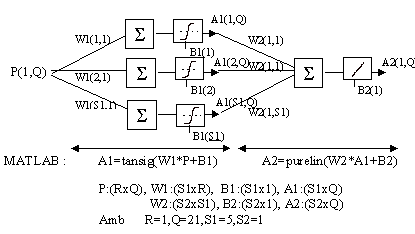
Fig. 11 Xarxa neuronal per aproximar la funció anterior
Per la implementació pots utilitzar les funcions següents de la ToolBox de Xarxes neuronals de Matlab :initff - Per la inicialització de la xarxa
trainbp - Per l’entrenament de la xarxa d’acord amb l’algorisme Backpropagation.
simuff - Per simular el comportament de la xarxaPer exemple, per la xarxa dela figura anterior, podem inicialitzar els pesos i bias fent :
S1 = 5;
[w1,b1,w2,b2] = initff(P,S1,'tansig',T,'purelin');Per l’entrenament cal definir una sèrie de paràmetres :
df = 10; % Frequency of progress displays (in epochs).
me = 8000; % Maximum number of epochs to train.
eg = 0.02; % Sum-squared error goal.
lr = 0.01; % Learning rate.Per l’entrenament de la xarxa amb els paràmetres anteriors executaríem la comanda següent :
tp = [df me eg lr];
[w1,b1,w2,b2,ep,tr] = trainbp(w1,b1,'tansig',w2,b2,'purelin',P,T,tp);i el resultat retornat son els pesos finals de cada capa i l’evolució de l’error a cada època. Finalment l’error es pot visualitzar fent :
ploterr(tr,eg);
Un cop entrenada la xarxa, prova el seu funcionament observant la sortida per un valor pel que no ha estat entrenada (dintre el marge compres entre -1 i 1) i compara la sortida amb la que dóna la funció original.
Nota : La matriu P, ha de contenir els 21 patrons (entrades) . Cada columna correspon a un patró (en aquest cas una columna només te un element) diferent. Per tant en aquest cas ha P sera un vector fila de 21x1.
3. Aplicació de les Xarxes Neuronals al reconeixement de patrons
Es desitja dissenyar i entrenar una xarxa neuronal que sigui capaç de reconèixer les 26 lletres de l’alfabet. Es suposa que es disposa d’un sistema de visió artificial capaç de digitalitzar cada lletra centrada en el camp de visió del sistema de reconeixement. El resultat d’aquesta digitalització es representa mitjançant una graella de 5 x 7 pixels boleans. El problema però apareix pel fet de què el sistema de visió artificial no és perfecte i junt amb la lletra digitalitzada s’hi afegeix soroll. Es pretén crear un sistema capaç de classificar les 5x7 entrades de forma que doni a la sortida la lletra corresponent. Prova la solució de Matlab en la demo anomenada neural. Executa :
>> neural