ALGORISMES GENÈTICS

 
 
 
 
 

Josep Lluís de la Rosa i Esteva
Departament d’Electrònica, Informàtica i Automàtica
peplluis@eia.udg.es

 

Introducció als GA.

Definició i ús dels GA.

Els algorismes genètics emulen el comportament de la naturalesa per poder resoldre aquells problemes prou complexes que els algorismes tradicionals no poden sol.lucionar o no troben solucions prou acurades.

Principi dels GA.

Els algorismes genètics intenten imitar la teoria de l'evolució de Darwin, on cal que una població conservi tot allò que sigui favorable per la seva supervivència i descarti tot el que li presenti debilitat d'adaptació. L'algorisme genètic farà que el conjunt de solucions s'adapti el millor possible i evolucioni després de diferents generacions cap a la solució.

D'on prové el nom de GA ?

Els algorismes genètics deuen el seu nom a les seves propietats bàsiques : selecció, creuament, herència i mutació.

Propietats més importants d'un GA.

La selecció és indispensable per escollir els individus de la població més capacitats. El creuament aportarà variabilitat als inividus de la nova generació. L'herència és necessària per transmetre les millores de les generacions pares a filles. La mutació permet en gran mesura el poder evolucionar cap a la solució desitjada quan la població es caracteritza per una manca d'aptituds, proporcionant-la de diversitat.

Funcionament bàsic d'un GA.

El funcionament bàsic d'un algorisme genètic és el d'evolucionar, a partir d'una població inicial d'individus, cap a una altra població d'individus amb unes característiques desitjades.
 

 
La població inicial es genera de manera aleatòria i cal una funció heurística o fitness per evaluar les aptituds dels individus enfront la solució on es vol arribar, és a dir, cal mesurar el grau de semblança o afinitat dels individus de la població amb els de la població final desitjada. El que és clar és que amb aquest primer pas no n'hi ha prou per arribar a la solució i cal generar més poblacions a partir de l'actual. Per això cal realitzar una selecció dels individus millor predisposats, és a dir, els que s'acosten més cap a la solució. Aquests individus escollits seran els pares de la següent generació i s'encarregaran de generar una nova població que heredi el millor d'aquests. La nova població estarà en terme mig més aprop de la solució que l'anterior i repetint aquest procés és una de les principals raons perquè hi hagi una convergència cap a la solució.

Cal notar però que, si cap individu de la població inicial presenta una característica desitjada per la solució no es convergirà mai cap a aquesta. Així cal que hi hagi un grau de diversitat a cada població i això ho proporcionarà la mutació.
 

Un GA bàsic.

Objectiu i paràmetres.

L'objectiu és el de que generació a generació els individus estiguin més aprop de la solució del problema que es planteja. Els paràmetres de l'algorisme genètic són : tamany de la població, tamany dels individus, nombre de generacions, probabilitat de creuament, probabilitat de mutació i determinar la funció d'adaptació.

Representació de les dades.

Les dades necessàries per un algorisme d'aquest tipus són una població de n individus. Cada individu estarà representat per una cadena de caràcters, de longitud m, que representaran els cromosomes de l'individu. Els components d'aquest vector de caràcters cadlfrà definir-los sobre algun conjunt de símbols o alfabet W . De manera semblant a la naturalesa cada component del cromosoma serà un gen, el valor d'aquest gen es definirà com al.lel i la seva posició dins la cadena com locus.

 

La codificació dels cromosomes és molt depenent del problema a resoldre. És molt important un bon dimensionament dels cromosomes per tal de que els valors que codifiquin permetin abarcar tots els valors produïbles al problema a resoldre i donin la precisió necessària per arribar a trobar la solució, permetent a l'algorisme convergir més eficientment i donar una solució més acurada. Segons aquesta idea també cal pensar en l'efecte contrari, si no es desitja tanta precisió a la solució, amb pocs gens al cromosoma farà que l'algorisme genètic estalvii temps de procés innecessari i reduïm la complexitat del problema. Cal recordar que, segons l'exemple anterior, amb un alfabet W _0,1 es poden codificar 2¹⁵ valors.

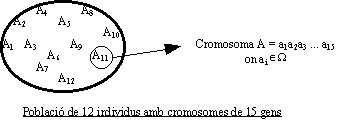
Recordem que els cromosomes han de contenir d’alguna manera informació sobre la solució del problema que representen. La codificació més usada és la d’una cadena de bits. Així podríem tenir per exemple :

Cada cromosoma és una cadena de bits i cada bit dins la cadena pot representar alguna característica de la solució. Hi ha però moltes maneres de codificació (nombres reals, permutacions, …) i depenen molt del problema a resoldre : reals,

Funcions adicionals.

Per a escollir els cromosomes amb més aptituds cal una funció heurística que ens evalui l'afinitat cada cromosoma a la solució. Si estem treballant amb un problema que té una funció objectiu, la funció d'adaptació (fitness) serà la mateixa que la funció objectiu. Així, cada individu de la població el formaran parells comosoma-valor d'adaptació.

Operadors bàsics.

L'operador de selecció s'encarrega de seleccionar els individus més aptes perquè intervinguin en la reproducció per a formar la següent generació. Cal que cada individu sigui evaluat amb la funció d'adaptació i se li assigni una probabilitat de selecció, obtinguda de dividir el seu valor d'adaptació entre la suma dels valors d'adaptació de tots els individus de la població.

L'operador de creuament s'encarrega de creuar els individus de dos en dos segons una determinada probabilitat de creuament. Llavors s'intercanvien entre els dos individus uns determinats gens que es poden escollir aleatòriament. Aquest intercanvi pot fer-se des d'una posició k fins al final del cromosoma o des de l'inici dins a una posició k del cromosoma. Un exemple de creuament seria el següent :

L'operador de mutació consisteix en alterar amb una probabilitat de mutació cadascun dels gens dels individus. Aquest operador aporta variabilitat ja que permet l'aparició de certs al.lels als inidividus que els anteriors operadors no poden generar si no apareixen aquests a la població inicial. Un exemple de mutació seria el següent :

Algorisme d’exemple.

3 Un GA bàsic en JAVA

3.1 La implementació d'un GA en JAVA.

El següent llistat constitueix un algorisme genètic bàsic implementat en JAVA. Els comentaris sobre l'algorisme estan marcats en negreta.

// Genetic Algorithm Java classes
// Copyright 1996, Mark Watson. All rights reserved.
package mwa.ai.genetic;
import java.util.*;
// Classe del genètic
public class Genetic extends Object {
protected int NumGenes; // Nombre de gens per cromosoma
protected int NumChrom; // Nombre de cromosomes de la població
protected BitSet Genes[]; // Conjunt de cadenes de gens que formen els
// cromosomes de la població
protected float Fitness[]; // Conjunt de valors d'adaptació dels individus
// constructor de classe
public Genetic() {
System.out.println("In dummy Genetic constructor");
// inicialització del tamany de cromosomes i de gens
NumGenes = NumChrom = 0;
}
// inicialització del genètic
public void init(int g, int c) {
System.out.println("In Genetic::init(...)");
Genes = new BitSet[c];
// generació dels comosomes de la població
for (int i=0; i<c; i++) {
Genes[i] = new BitSet(g);
for (int j=0; j<g; j++) {
// generació d'un cromosoma de forma aleatòria
if (Math.random() < 0.5) Genes[i].set(j);
}
}
NumChrom = c;
NumGenes = g;
Fitness = new float[c];
// valor d'adaptació inicial molt negatiu per a tots els cromosomes
for (int f=0; f<c; f++) Fitness[f] = -999;
Sort(); // classificació dels individus pel seu fitness
}
// obtenció de l'al.lel d'un gen d'un inidividu de la població
public boolean GetGene(int chromosome, int gene) {
return Genes[chromosome].get(gene);
}
// assignar un al.lel a un gen d'un individu de la població
public void SetGene(int chromosome, int gene, int value) {
if (value == 0) Genes[chromosome].clear(gene);
else Genes[chromosome].set(gene);
}
public void SetGene(int chromosome, int gene, boolean value) {
if (value) Genes[chromosome].set(gene);
else Genes[chromosome].clear(gene);
}
// classificar els individus pel seu valor d'adaptació per a ser
// seleccionats pel creuament
public void Sort() {
BitSet btemp;
for (int c=0; c<NumChrom; c++) {
for (int d=(NumChrom - 2); d>=c; d--) {
if (Fitness[d] < Fitness[d+1]) {
btemp = Genes[d];
float x = Fitness[d];
Genes[d] = Genes[d+1];
Fitness[d] = Fitness[d+1];
Genes[d+1] = btemp;
Fitness[d+1] = x;
}
}
}
}
// operador creuament
public void DoCrossovers(double rate) {
// rèplica de la meitat dels millors individus sobre l'altra meitat
for (int m=0; m<NumChrom/2; m++) {
CopyGene(m + NumChrom/2, m);
}
// rèplica del material genètic dels dos millors individus
for (int i=0; i<NumGenes; i++) {
SetGene(NumChrom - 1, i, GetGene(0, i));
SetGene(NumChrom - 2, i, GetGene(0, i));
SetGene(NumChrom - 3, i, GetGene(0, i));
SetGene(NumChrom - 4, i, GetGene(1, i));
SetGene(NumChrom - 5, i, GetGene(1, i));
}
// el nombre de creuaments dependrà de la probabilitat de creuament
int num = (int) (NumChrom * rate);
for (int i=0; i<num; i++) {
// seleccionar dos cromosomes al.leatòriament (els dos millors
// cromosomes no es creuen i es conserva el seu material genètic)
int c1 = 2 + (int)((NumChrom - 2) * Math.random() * 0.99);
int c2 = 2 + (int)((NumChrom - 2) * Math.random() * 0.99);
if (c1 != c2) {
// determinar un locus on finalitzar l'intercanvi de gens
int locus = 2 + (int)((NumGenes - 3) * Math.random());
// intercanvi de gens entre els dos cromosomes
for (int g=0; g<locus; g++) {
boolean temp = GetGene(c1, i);
SetGene(c1, i, GetGene(c2, i));
SetGene(c2, i, temp);
}
}
}
}
// còpia de gens d'un individu a un altre
private void CopyGene(int to, int from) {
for (int i=0; i<NumGenes; i++)
if (GetGene(from, i)) SetGene(to, i, 1);
else SetGene(to, i, 0);
}
// operació de mutació
public void DoMutations() {
int c = 2 + (int)((NumChrom - 2) * Math.random() * 0.95);
int g = (int)(NumGenes * Math.random() * 0.95);
if (GetGene(c, g)) SetGene(c, g, 0);
else SetGene(c, g, 1);
}
// càlcul de la funció d'adaptació segons el problema a resoldre
public void CalcFitness() {
}
}
/* fi del llistat */
 
 

3.2 Comentaris.

La selecció en l'algorisme genètic anterior estaria implementada de la següent manera : caldria evaluar la funció d'adaptació per a cada individu de la població i ordenar els individus descendentment pel seu valor de fitness.

El creuament també funciona de forma diferent. No existeix una probabilitat de creuament global ni una probabilitat de selecció per a cada individu. Aquí, la meitat millor dels inidividus es duplica i es descarta l'altra meitat. Llavors es copia el millor individu tres vegades i el segon millor individu dues sobre els cinc pitjors individus. Finalment es realitza un nombre de creuaments igual a la quarta part de la població amb la restricció de que una rèplica dels dos millors individus no es creua mai.

La mutació també funciona diferent. En comptes de definir una probabilitat de mutació i aplicar-la a tota la població es realitza un nombre de mutacions sobre el total de la població.

Anàlisi dels GA

Què cal tenir en compte en un GA ?

Cal que el nombre d'indivius de la població i el nombre de cromosomes dels individus sigui prou acurada. Cal ajustar aquests dos paràmetres el més alts possibles perquè l'algorisme convergeixi correctament a la solució i no caigui en màxims locals, si bé cal tenir en compte que augmentarà el temps de càlcul de l'algorisme i per tant el temps en trobar la solució. Un nombre d'individus prou alt assegurarà l'aparició de més esquemes o patrons genètics. Un nombre de gens prou alt permetrà codificar amb més precissió les dades que representen els gens i aportarà una solució més acurada. Normalment es treballa amb l'ordre de 100 individus de 20 a 30 gens per comosoma.

La probabilitat de creuament ha de ser prou alta perquè la mitja de valors objectiu s'estabilitzi després d'un nombre inicial de generacions. Els valors de treball adequats estan normalment entre el 75% i 95%.

La probabilitat de mutació ha de ser prou baixa perquè no afecti als bits més significatius en massa mesura. Els valors de treball adequats oscil.len entre el 0,5% i l'1%.

Propietats d'un GA.

Un algorisme genètic es caracteritza perquè no ha de recòrrer tot l'espai de cerca per trobar una bona solució. La rel.lació de les probabilitats de selecció i creuament enfront la de mutació determinen el compromís de com recòrrer el graf de cerca : quan prengui major importància l'operació de mutació s'explorarà l'espai de cerca en diferents hiperplans (cerca per amplitud), mentre que a la inversa, s'explotarà un hiperplà de cerca (cerca en profunditat).

Aplicacions dels GA.

• Nonlinear dynamical systems - predicting, data analysis
• Designing neural networks, both architecture and weights
• Robot trajectory
• Evolving LISP programs (genetic programming)
• Strategy planning
• Finding shape of protein molecules
• TSP and sequence scheduling
• Functions for creating images

Els Cromosomes

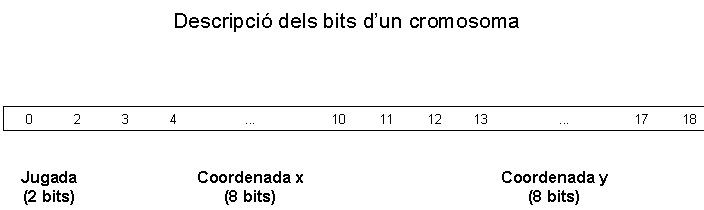
En aquest cas els cromosomes codifiquen possibles jugades. Cada possible jugada es codifica amb un codi de jugada i una posició. El codi de jugada és un enter codificat amb dos bits. La posició de la jugada esta formada per dos números reals que equivalen a la coordenada x i la coordenada y respectivament. Per tant cada cromosoma conté la següent informació: