Introducció
En aplicacións de robòtica generalment és necessari controlar les característiques dinàmiques d’un sistema perquè compleixi amb un conjunt d’especificacions.Estratègies de controlAlguns dels exemples més comuns són el control de velocitat d’un motor o el posicionament d’algun element mecànic.
Molt sovint la variable controlada (velocitat, posició) ha de mantenir-se en l’interior d’un cert marge encara que el sistema estigui subjecte a pertorbacions externes: el braç d’un robot manipulador ha de seguir una determinada trajectòria sempre encara que el valor de la càrrega canviï.
Com a primer exemple, considerem que es pretén controlar la velocitat de gir d’un motor de DC. El motor, sistema a controlar, s’anomena procés o planta.
Anem a suposar un model senzill on la velocitat de gir del motor de DC és proporcional al voltatge aplicat, es a dir: omega = K×v

Si el que es pretén és controlar la velocitat de gir només cal aplicar un voltatge per a cada velocitat, a partir d’una taula o amb un càlcul v = omega/K i obtenir el voltatge necessari.
Aquesta manera d’operar se’n diu en llaç obert, el fet de treballar així pot comportar alguns problemes com ara, si varia la càrrega o el fregament segurament per a un determinat voltatge la velocitat de rotació ja no serà la mateixa
El problema del llaç
obert és que no hi ha percepció, es pot afirmar que un llaç
obert opera en la foscor.
Una possible solució
pot ser conèixer la pertorbació (canvi de càrrega,
canvi de fregament, etc...) i fer una correcció del voltatge en
funció del valor de la pertorbació. Aquesta idea es coneix
com a control feedforward.
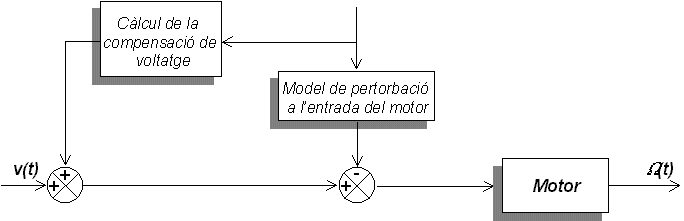
Finalment l’altra estratègia
de control i segurament la més important consisteix en mesurar la
velocitat de sortida del motor i fer una comparació amb la velocitat
de sortida adaptant el voltatge fins aconseguir la velocitat desitjada
Aquesta última estratègia es coneix com a llaç tancat o realimentació (closed-loop control or feedback).
L’esquema d’aquest control correspon al de la figura següent:
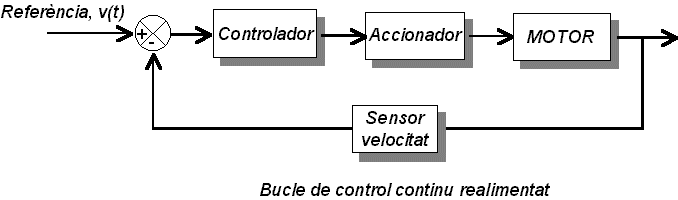
La representació anterior correspon a un bucle de control, però quins són els senyals i components que intervenen en un bucle de control ??
Per això seguim sobre l’exemple del motor
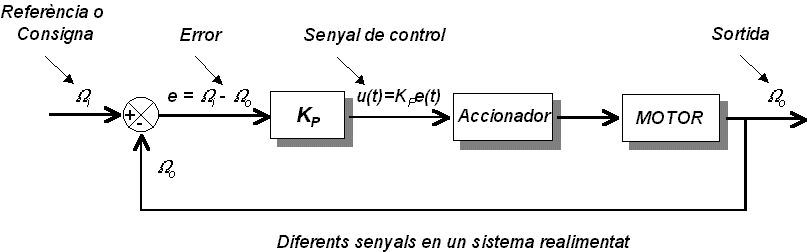
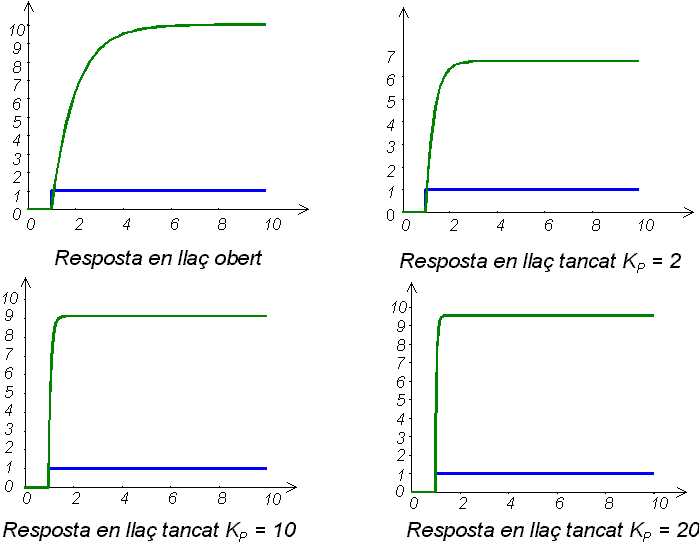
En aquest cas el tipus de controlador escollit és un proporcional, la seva sortida és proporcional al senyal d’error. Quan més gran és l’error més enèrgica és l’acció del controlador.
Aquest controlador no pot fer que l’error sigui nul, perquè per a una determinada sortida del controlador ha d’existir un error determinat
Podríem disminuir l’error augmentant K, però això donaria lloc a inestabilitat.
Resposta temporal en llaç obert i amb controlador P
Control Proporcional+Integral
Com s’ha vist el principal inconvenient d’un controlador amb acció proporcional, és que sempre deixa un error per corregir, més gran quan menor és KP. L’acció integral permet anul·lar aquest error fent que el senyal de control, u(t), creixi proporcionalment al producte (error×temps). Es pot afirmar que, en un sistema amb acció integral tendeix a anul·lar l’error promig. Això es pot expressar en els diagrames de blocs següents:
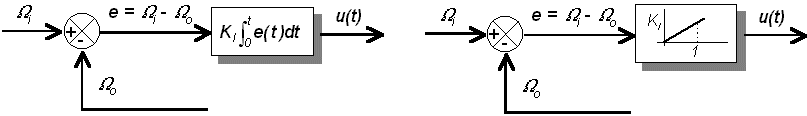
La constant Ki s’anomena
constant integral i la seva inversa Ti, s’anomena constant de temps integral.
Com s’ha vist l’acció
integral elimina l’error en estat estacionari però alenteix la resposta
dinàmica, es per això que aquest control s’aplica amb un
proporcional parlant així de control PI

Acció derivativa
Les accions proporcional i integral no permeten resoldre de forma satisfactòria tots els problemes de control. De la primera hem dit que deixa sempre un error permanent i de la segona que pot causar inestabilitat o excés de temps de resposta. L’acció derivativa complementa a les dues anteriors ajudant a obtenir una resposta dinàmica més ràpida (temps de resposta menor).
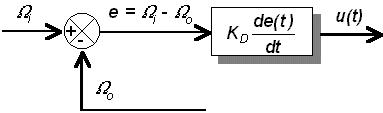
En aquest cas KD s’anomena constant d’acció derivativa. L’acció derivativa s’utilitza juntament amb altres, atès que quan l’error és nul no dona sortida.
Es pot afirmar que l’acció derivativa afegeix una amplificació de les variacions, per tant, proporciona una amplificació extra en els transitoris, fent que la resposta sigui més enèrgica.
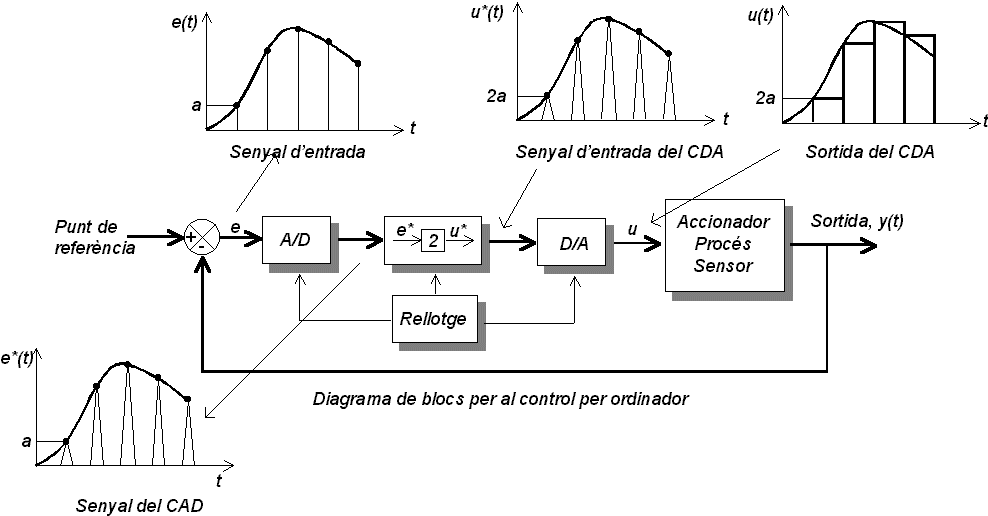
Control per ordinador