Resumen: En los últimos años el tratamiento de sistemas robóticos móviles y cooperantes se ha basado en el paradigma agente. Tanto en las técnicas de análisis y diseño como en los algoritmos de decisión individual y colectiva de estos sistemas, no se tienen en cuenta las ecuaciones diferenciales que describen la dinámica del movimiento de los robots. En este trabajo se presentan algunos resultados encaminados a introducir dichas ecuaciones en la toma de decisiones individuales y colectivas de dichos agentes. Para ello se ha extendido la interpretación del agente de Shoham no ya como agente físico sino como agente físico con una dinámica propia la cual conlleva que ciertas acciones sean realizables y otras no.

I. INTRODUCCIÓN

El campo de la robótica móvil está asistiendo a una emergente cantidad de trabajos relacionados con la problemática del trabajo cooperativo en sistemas multi-robot gracias a la introducción del paradigma agente como herramienta de análisis y diseño, y a su inminente aplicabilidad. Sin embargo, aunque la introducción de dicha técnica de inteligencia artificial permita resolver problemas complejos mediante cooperación, no tiene en cuenta que su aplicación en robots móviles necesita que el agente físico sea capaz de controlar el cuerpo físico asociado, es decir, ejecutar trayectorias correctamente, seguir y evitar objetos, etc. De hecho, cualquier tarea por simple que sea contiene infinitas situaciones debido a los continuos cambios del entorno y a los propios movimientos del robot-agente, o también llamados acciones. Los estudios con robots reales como [1], [2], [3]

se dedican a testear diversas técnicas de negociación y protocolos de comunicación mientras que los problemas que causan las dinámicas de los robots se interpretan desde el punto de vista de supervisión y de detección de fallos. Es decir, son problemas que se analizan a posteriori y no en la etapa inicial de análisis.

El diseño de los controladores incorporados en los sistemas autónomos realimentados (robots móviles) se hace teniendo en cuenta diversas especificaciones en la respuesta del sistema ante diversos tipos de entradas. En este trabajo se mostrará que hay situaciones en que este tipo de análisis puede ser insuficiente puesto que no se tienen en cuenta ciertos aspectos dinámicos que pueden ser importantes no ya en la respuesta del sistema, sino en consecuencias físicas derivadas. Por tanto, aunque la decisión del agente sea correcta desde un punto de vista lógico, la ejecución de la acción correspondiente conllevará consecuencias no deseadas.

Este trabajo se centra en como evitar los problemas que se derivan del proceso de decisión cuando no se utiliza la información del mundo físico, en concreto, la información relativa a las características dinámicas del sistema físico subyacente al agente. A modo de ilustración, se utilizará un ejemplo de un convoy formado por dos vehículos autónomos: el problema que se planteará se concentra en cómo controlar la velocidad del segundo vehículo de forma que mantenga una cierta distancia de seguridad con el primero. Para la resolución de esta problemática se propone ampliar la noción del agente de Shoham [4] incluyendo parámetros dinámicos en las capacidades. Así, se obtiene un agente físico conocedor de su dinámica de forma que sus limitaciones físicas pueden influir en la toma de decisiones e inhibirlas en caso que supongan acciones no realizables. Esta ampliación supone una mejora cualitativa respecto a la que se introdujo en [5] en dónde el proceso de decisión incluía un parámetro de certeza que aparecía de forma natural puesto que el método de razonamiento estaba basado en lógica fuzzy. En este trabajo, independientemente del método de razonamiento, también aparecerá un parámetro de certeza indicativo del grado de precisión de la acción de control, que está completamente vinculado a las características dinámicas del sistema físico (cuerpo físico) del agente.

II. EL PROBLEMA DE LA COLISIÓN EN UN CONVOY

Sea un sistema formado por dos vehículos (A y B) que circulan en línea recta y con velocidades independientes. El problema de control que se plantea es como controlar la velocidad del vehículo de atrás (V_B) de forma que mantenga una cierta distancia de seguridad (D) ante variaciones de V_A. Desde un punto de vista lineal, la dinámica de este sistema convoy controlado es como sigue: el sistema A es el guía, y dispone de un sistema de control aparentemente independiente de B. El segundo vehículo tiene una estructura inherentemente más compleja puesto que el mantenimiento de la formación está completamente bajo su responsabilidad. Asumiendo que los sistemas A y B presentan ambos funciones de transferencia de primer orden en lazo cerrado (G_A(s) y G_B(s)), el comportamiento en situación de convoy del sistema B responde a un sistema de segundo orden (véase la figura 1). Este cambio cualitativo de dinámica en los sistemas convoy debe tenerse en cuenta para obtener un buen comportamiento en situación de formación.

La variable a controlar es V_B con la especificación de mantener una distancia regular D entre los dos sistemas autónomos. El problema se puede atacar con un controlador proporcional de forma que la señal de control sobre G_B(s) es: K_P´(D - (X_A-X_B)). En la figura 1 se muestra la evolución del sistema para las condiciones iniciales D=5m, V_A(t₀)=V_B(t₀)=8m/s, X_A(t₀)-X_B(t₀)=0, y con el cambio V_A(t=5)=4m/s. Como puede observarse, el comportamiento de V_B(t) es de segundo orden.

FIG.1: VELOCIDADES DE LOS MÓVILES A Y B

En el análisis previo no se ha hecho mención alguna sobre la posibilidad de colisión. Sin embargo, a causa de este comportamiento de orden superior parece razonable deducir que el uso de información sólo de tipo estático puede resultar insuficiente en las etapas de decisión agente-agente. Por tanto, la decisión basada únicamente en parámetros estáticos puede tener resultados peligrosos (colisiones, como en este ejemplo) cuando se aplica en agentes físicos dinámicos.

III. INTRODUCCIÓN DE PARÁMETROS DINÁMICOS EN LOS AGENTES

Existen dos tipos de comportamiento para los agentes: el reactivo y el deliberativo. En líneas generales, en un tipo reactivo el agente guía decidiría frenar o acelerar sin tener en cuenta la dinámica del otro agente y sería pura responsabilidad de éste el no colisionar. Este comportamiento se corresponde con lo que se ha mostrado en la sección anterior. Sin embargo, en el deliberativo los dos agentes pueden negociar e intercambiar información y el guía modifica su conducta basado en la opinión del otro. Así, cuando los parámetros dinámicos (y estáticos) de un agente no permitan la ejecución de la acción correspondiente, la decisión quedará inhibida y deberá ser negociada hasta llegar a un acuerdo. Por tanto, para basar la decisión en la dinámica de ambos agentes será necesario contar con su cooperación para que las decisiones se tomen conjuntamente. Para llevar a cabo esta idea se ha tomado como referencia el AGENT0 [4], un lenguaje de programación orientado a agentes: el agente queda especificado con diversos conjuntos de datos (capacidades, creencias y compromisos), y un conjunto de reglas de compromisos. El funcionamiento del agente se basa en la ejecución de estas reglas cuyos consecuentes son las acciones. Las acciones pueden ser comunicativas, las cuales permiten el intercambio de información, y privadas, correspondientes a los procesos internos del agente.

Este estudio se basa en incluir la dinámica de los vehículos añadiendo un subconjunto de capacidades. Estas nuevas capacidades se construyen a partir de los resultados de la simulación de la respuesta del sistema frente a un conjunto finito de consignas y con variaciones de los parámetros del controlador. Con estos resultados se crea una base de datos en donde constan, para cada consigna o ensayo, los parámetros dinámicos fundamentales de la respuesta, léase ganancia, tiempo de respuesta, parámetros de control, estabilidad, etc. De esta manera, cuando el agente guía comunique su intención de frenar o acelerar a una determinada velocidad podrá especificar directamente el tiempo requerido para llevarla a cabo, o la precisión de su ejecución u otros datos dinámicos de interés para la resolución del problema. Para sistemas de primer orden como los presentados en la segunda sección, se han utilizado los siguientes parámetros para construir las capacidades:

TABLA 1. LISTA DE PARÁMETROS USADOS EN LA CONSTRUCCIÓN DE LAS CAPACIDADES DEL AGENTE.

En estas condiciones, el agente ‘A’ está en disposición de pedir al ‘B’ si un cambio de velocidad de V_I a V_F en un tiempo determinado puede producirse sin peligro de colisión.

IV. INTERCAMBIO DE PARÁMETROS DINÁMICOS: EJEMPLO CON EL CONVOY

Una vez se ha conseguido que el agente físico sea consciente de sus limitaciones físicas, debe ser capaz de usarlas en el proceso de decisión de acciones. Para ello hace falta establecer el mecanismo de negociación y usar las acciones comunicativas para permitir el intercambio de información. De las acciones comunicativas inicialmente propuestas en AGENT0, aquí se utilizarán dos: request y inform, y respecto a las acciones privadas sólo se han definido dos: ‘frenar’ y ‘acelerar’, pero matizadas con la introducción de los parámetros dinámicos.

En cuanto al subconjunto de capacidades, se han ordenado de forma que cada capacidad quede especificada con el siguiente conjunto de parámetros: {specified_time_for_action, initial_state, final_state, certainty}. La variable specified_time_for_action t_d se define como un múltiplo (3 veces) de la constante de tiempo (t ) de la respuesta dinámica del sistema. El parámetro initial_state e_i se define como la velocidad inicial; el final_state e_f corresponde a la velocidad final; y certainty corresponde a un coeficiente calculado a partir del conocimiento de la dinámica y de la estática del sistema f(G(s),t_d,e_i,e_f). Por ejemplo, se podría definir este coeficiente a partir de la constante de tiempo y del error del sistema en estado estacionario. En sistemas más complejos se pueden definir coeficientes más elaborados: para la ejecución de trayectorias 2D libres de colisión se puede usar un índice de la dificultad de ejecución de dicha trayectoria [6].

Respecto al mecanismo de negociación, a continuación se muestra como funciona el protocolo de comunicación entre los agentes A y B para el caso SP_A<0, es decir, cuando el guía decide ejecutar la acción ‘frenar’ (en cursiva se muestran los parámetros dinámicos):

(i) ‘A’ decide cambiar su velocidad y pide confirmación a ‘B’:

request( A, B, v_init_A, v_fin_A, time, t_A, e_SS)

(ii) ‘B’ recibe el mensaje y procesa la información:

Cálculos previos: SP_A= v_fin_A - v_actual_A

Acción privada (procedimiento de búsqueda)

IF_EXISTS Essay WITH SPÎ[SP_A- e_SS , SP_A+e_SS ]

THEN SELECT Essay

t_B = t (#Essay)

e_SS_B = e_SS(#Essay)

ELSE [t_B, e_SS _B]=calculate_time(SP_A, time)

END

Acción comunicativa

IF t_B<t_A

THEN inform( B, A, v_fin_A, time)

do( B, v_fin_A, time)

ELSE request( B, A, v_fin_A, t_B, e_SS _B )

END

(iii) ‘A’ recibe la respuesta. Si ‘B’ inhibe la acción se negocia t :

IF answer IS_TYPE ‘inform’

THEN do( A, v_fin_A, time)

ELSE [t_A, e_SS _A]=calculate_time( SP_A, 4´ (t_B+t_A)/2) inform( A, B, v_fin_A, time, t_A, e_SS_A)

do( A, v_fin_A, time)

END

Descripción: una vez el guía inicia la comunicación, el otro agente busca entre sus capacidades si puede cumplir con los requisitos dinámicos y, en caso afirmativo, confirma la decisión. En caso contrario simula su comportamiento con los datos provistos por el agente guía y le confirma que puede realizar la acción pero con un tiempo y una precisión diferentes. Basándose en esta información, el guía decidirá si ejecutar o negociar la acción decidida. Aunque el mecanismo de negociación podría llegar a ser muy complejo, se ha optado por una solución de compromiso: cuando los tiempos de respuesta son inadecuados se impone un tiempo promedio para ambos.

V. RESULTADOS

En el ejemplo que se muestra a continuación se utilizarán dos móviles en formación de convoy cuyas velocidades quedan representadas a partir de las siguientes funciones de transferencia:

En una primera simulación se supondrá que el agente ‘A’ toma sus decisiones de forma completamente independiente del agente ‘B’ lo cual conllevará a situaciones de riesgo o incluso de peligro inminente. Por falta de espacio en este artículo, en este apartado sólo se mostrará una situación de peligro. Al final, se verá cómo mejora el resultado de la simulación con la introducción del mecanismo de negociación mostrado en la sección anterior.

Supongamos que el agente ‘A’ decide frenar hasta una velocidad de 2m/s menor a la actual. Por su parte el agente ‘B’ deberá reaccionar a dicho cambio de velocidad y mantener la especificación estática de la distancia de separación entre ambos (D>0). Es decir, estamos suponiendo un comportamiento reactivo de ambos agentes.

Se puede comprobar que la decisión de frenar no se podrá llevar a cabo debido a una colisión previa a la llegada al estado estacionario de los dos sistemas (véase la figura 2). Tal y como se ha discutido anteriormente, las causas de dicha colisión están en las diferencias entre las dinámicas de los dos sistemas, representadas por medio de sus funciones de trasferencia. Por otra parte, desde un punto de vista agente, el agente ‘B’ debe ser consciente (deberá tener la capacidad de introspección) de sus limitaciones dinámicas e informar de ello al otro agente.

Por lo tanto, la decisión de frenar ya no es responsabilidad exclusiva ni del agente ‘A’ ni del ‘B’, sino de los dos.

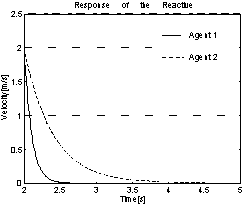
FIG. 2: RESPUESTA DE AGENTES REACTIVOS. HAY COLISIÓN.

Para obtener resultados con agentes deliberativos, la decisión deberá ser cooperativa, es decir, tendrá que haber intercambio de información entre los dos agentes. Sin embargo, para definir el método de negociación entre ambos se debe especificar sobre qué se negocia. En este experimento la negociación busca un acuerdo con el parámetro t (véase ‘Descripción’ en la sección anterior) y con la ayuda del parámetro certainty: cuando una capacidad ofrece un certainty inferior al 0.6 se inhibe. Cabe comentar en este punto que la negociación podría ser más elaborada con el uso de más parámetros (dinámicos y estáticos).

A continuación se presenta la misma situación que en el caso anterior pero resuelto con agentes deliberativos: el agente ‘A’ decide parar con t=0.3s. Después que el agente ‘B’ inhiba la ejecución a causa de su baja fiabilidad (0.52), acuerdan un valor t=0.6s puesto que ‘B’ obtiene una fiabilidad superior (0.77). Puede observarse que la distancia no se anula, es decir, se evita la colisión (véase la figura 3).

FIG. 3: RESPUESTA DE AGENTES DELIBERATIVOS. SE EVITA LA COLISIÓN.

En este ejemplo cabe comentar que los controladores son los mismos que en el caso reactivo sólo que con una mejor decisión mutua entre agentes.

Los resultados que se han mostrado son suficientes para comprobar que el funcionamiento del sistema en su conjunto es mejor. De hecho, la mejora de la decisión se debe al hecho que los agentes se intercambian información relativa a la fiabilidad sobre sus capacidades, es decir, pueden suministrar un índice de bondad de la decisión.

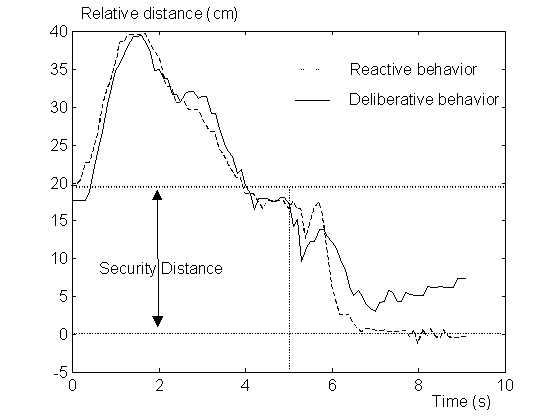
FIG. 4: EVOLUCIÓN DE LA DISTANCIA DE LOS AGENTES

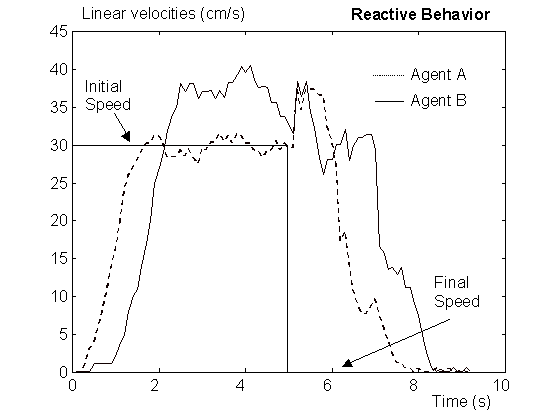
FIG. 5: VELOCIDAD DE LOS AGENTES EN EL CASO DE DECISIÓN REACTIVA

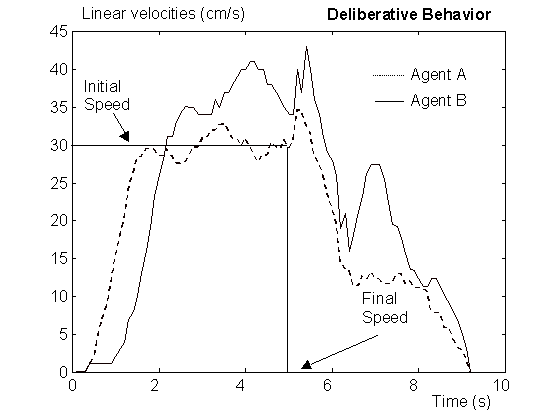
FIG. 6: VELOCIDAD DE LOS AGENTES EN EL CASO DE DECISIÓN DELIBERATIVA

VI. CONCLUSIONES Y TRABAJO FUTURO

El análisis de los sistemas reales multi-robot en trabajo cooperativo presenta una gran cantidad de problemas si se hace hincapié en los fenómenos físicos del sistema global (agentes + entorno). La motivación de este trabajo es poder establecer un método de diseño que tenga en cuenta que el sistema en conjunto está formado por subsistemas autónomos con dinámicas propias. En la Universitat de Girona se está llevando a cabo un proyecto con micro-robots móviles reales que cooperan para desplazar objetos grandes. En este caso los problemas ocasionados por la dinámica de los robots son mucho más complejos que los presentados en este trabajo ya que hay colisiones de diversos tipos y cambios en las dinámicas de los robots cuando entran en contacto con los objetos que han de empujar. El presente estudio permite asegurar que la introducción de parámetros dinámicos en el conjunto de las capacidades del agente permite obtener un mejor comportamiento colectivo de los robots.

Aunque hay más problemas a analizar como los derivados de las limitaciones que impone la ejecución del proceso en tiempo real, queda por analizar qué tipos de parámetros deberían usarse para sistemas con componentes no lineales o con dinámicas de orden superior. En este caso la negociación debería ser más compleja puesto que el sistema podría ser no homogéneo ya que las dinámicas no serían comparables.

VII. AGRADECIMIENTOS

Este trabajo ha sido parcialmente financiado por el proyecto CICYT TAP98-0955-C03-02 "Diseño de agentes físicos (DAFne)" del MEC y por 1999GR00161 "Grup de Recerca Consolidat de Sistemes Integrats" CIRIT del Gobierno Catalán.

VIII. REFERENCIAS

R.Beckers, O.E.Holland, and J.L.Deneubourg. "From Local to global tasks: Stigmergy and collective robotics". Proc. A-Life IV. MIT Press, 1994.
McFarland. "Towards robot cooperation". Proc. Simulation of Adaptive Behavior, 1994.
L.Steels. "A case study in the behavior-oriented design of autonomous agents". Proc. Simulation of Adaptive Behavior, 1994.
Y. Shoham. "Agent-oriented programming". Artificial Intelligence, 60:51-92, 1993.
J.Ll. de la Rosa, A. Oller, J.Vehí, J.Puyol. "Soccer Team based on Agent-Oriented Programming". Robotics and Autonomous Systems. 21 (1997) 167-176. Ed. Elsevier B.V. 1997.
A. Oller, J.Ll. de la Rosa, R.García, J.A.Ramon, A.Figueras. "Micro-Robots Playing Soccer Games: A Real Implementation Based on Multi-Agent Decision-Making Structure". Intelligent Automation and Soft Computing. En prensa. 1999.

VIII. CURRICULA

Josep Lluís de la Rosa es Doctor en Ciencias por la Universidad Autónoma de Barcelona desde 1993 http://eia.udg.es/~peplluis. Tras consecutivas estancias pre y postdoctorales en Francia, es el director del grupo de investigación eXiT, Ingeniería de Control y Sistemas Inteligentes, desde el 1994, http://eia.udg.es/exit. Sus trabajos más conocidos son los agentes físicos y especialmente los relacionados con los desarrollos con robots futbolistas, http://rogiteam.udg.es

Josep Antoni Ramon es Ingeniero en Automática por la Universidad Politécnica de Cataluña. Actualmente es profesor asociado. La investigación se centra en el ámbito de la supervisabilidad de los agentes físicos mediante técnicas de sistemas híbridos.